Support Vector Machine (SVM)
Support Vector Machine (SVM) is a promising model for classification of both linear and nonlinear data. SVM uses nonlinear mapping to transform the linear dataset into a higher dimension. In this dimension it searches for the linear optimal separating hyperplane. A hyperplane is a decision boundary to separate two classes. Support vectors are the essential training tuples from the set of training dataset. With a sufficiently high dimension and appropriate nonlinear mapping two classes can be separated with the help of support vectors and margins defined by the support vectors. Training of SVM is slow, but is very accurate due to their ability to model nonlinear decision boundaries. This is why SVM has been selected to classify the given dataset.
Linear SVM
To explain Linear SVM it is necessary to consider a dataset D be given as [(X1, y1), (X2, y2), …… , (X|D|, y|D|)], where Xi is the set of training tuple with the corresponding class label yi. Each of the class labels yi can take either +1 or -1 corresponding to the training tuple. Then the study needs to search the separating hyperplane. There are infinite numbers of hyperplanes that can exist in between the two class labels. In SVM it is needed to search the maximum marginal hyperplane (MMH) as illustrated below in Figure 1.
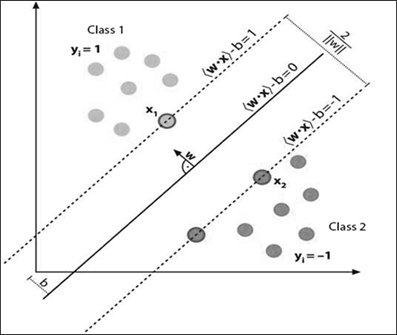
Figure 1: A SVM showing maximum marginal hyperplane between two classes
Here, Figure 1 considers all the possible hyperplanes and their possible margins. A margin is the shortest distance between the hyperplane and one of the sides, where the side is parallel to the hyperplane. For accurate classification it is likely to consider the maximum possible distance in between the margins. A separating hyperplane can be given as:
W.X – b = 0 ———> (1)
where W is the weight vector and b is the bias. Thus the tuples in the dataset can be sub-grouped into two classes with margins H1 and H2 as:
H1: W.X – b ≥ 1 for yi =+1 and H2: W.X – b ≤ 1 for yi =–1 ———> (2)
Thus the tuples that falls above H1 corresponds to the first class and the tuples that are below H2 are in the second class. If there exist any tuples that fall on either H1 or H2 , then they are the support vectors. It is important to note that the hyperplane is positioned in the middle of the two margins. Thus the maximum margin can be given as 2 / ||W||, where ||W|| is the Euclidean norm of W, that is √(W.W).
Nonlinear SVM
There are several nonlinear versions of SVM available. All of these are kernel based. The nonlinear version of a SVM can be represented by using a kernel function K as:
K(Xi , Xj) = φ(Xi) .φ(Xj) ———> (3)
1. Polynomial kernel:
For SVM, a Polynomial kernel of degree ‘d’ is defined as –
K(Xi , Xj) = (Xi.Xj + 1)d ———> (4)
2. Gaussian radial basis function kernel:
For SVM, a Gaussian radial basis function kernel is defined as –
K(Xi , Xj) = e-||(Xi – Xj)||2 / 2σ2 ———> (5)
3. Sigmoid kernel:
For SVM, a Sigmoid kernel is defined as –
K(Xi , Xj) = tanh(κXi.Xj – δ) ———> (6)